

- #Finding the vertex of a quadratic function how to#
- #Finding the vertex of a quadratic function plus#
The graph will have one of two shapes, and the a value tells which shape it will be. But if a = -1, then you get y = 2(x - (-1)) 2 - 3, which with just a teeny bit of simplification turns out to be your equation, so that must be right: a = -1. Name: Algebra 2 Date: Finding the Vertex Finding the Vertex Vocabulary and basic facts The graph of any quadratic function f(x) ax2 + bx + c is called a parabola.
#Finding the vertex of a quadratic function how to#
The answer is that if a = 1, you get y = 2(x - 1) 2 - 3, which is not your equation, so that must be wrong. This video explains how to find the equation of a quadratic function in vertex form given the vertex and a point on the parabola. Lesson Summary: This is an inquiry-based lesson designed to teach students how to find the.
Did you know that you can use the formula for the axis of symmetry. Lesson Title: Finding the Vertex of a Quadratic Function 2.
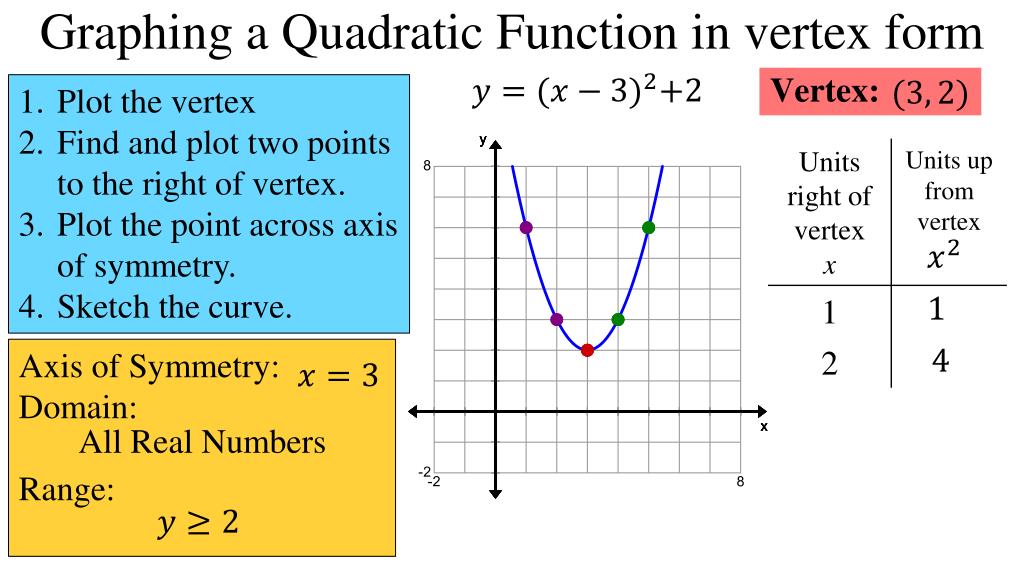
Write a step by step algebraic process that someone could use to find the vertex of a quadratic function that is written in vertex form. Note: The vertex of a quadratic equation is the minimum or maximum point of the equation. In this situation, you need to keep your cool, and ask the question, "What would a and b have to be in order to get the equation in the desired form?" It's clear that b = -3, and you got that part right, but now you are wondering whether a = 1 or a = -1. Make a conjecture about the relationship between the vertex of a quadratic function and the values of a, h and k in the vertex form of a quadratic equation.
#Finding the vertex of a quadratic function plus#
Anyway, now you have it almost into that form, except for that pesky plus sign where you want to see a minus. (I may not have gotten the letters k, a, and b right, but it doesn't matter. is a vertical parabola with axis of symmetry parallel to the y axis and has a vertex V with coordinates (h, k), x - intercepts when they exist and a y - intercept as shown below in the graph. I bet you're looking at a formula that says that if you get a quadratic in the form Review Vertex and Intercepts of a Quadratic Functions The graph of a quadratic function of the form.


 0 kommentar(er)
0 kommentar(er)
